- curl
-
—curledly /kerr"lid lee, kerrld"-/, adv. —curledness, n./kerrl/, v.t.1. to form into coils or ringlets, as the hair.2. to form into a spiral or curved shape; coil.3. to adorn with, or as with, curls or ringlets.v.i.4. to grow in or form curls or ringlets, as the hair.5. to become curved or undulated.6. to coil.7. to play at the game of curling.8. to progress in a curving direction or path; move in a curving or spiraling way: The ball curled toward the plate.9. curl one's or the hair, to fill with horror or fright; shock: Some of his stories about sailing across the Atlantic are enough to curl one's hair.10. curl one's lip, to assume or display an expression of contempt: He curled his lip in disdain.11. curl up, to sit or lie down cozily: to curl up with a good book.n.12. a coil or ringlet of hair.13. anything of a spiral or curved shape, as a lettuce leaf, wood shaving, etc.14. a coil.15. the act of curling or state of being curled.16. Plant Pathol.a. the distortion, fluting, or puffing of a leaf, resulting from the unequal development of its two sides.b. a disease so characterized.a. a vector obtained from a given vector by taking its cross product with the vector whose coordinates are the partial derivative operators with respect to each coordinate.b. the operation that produces this vector.18. Weight Lifting.a. an underhand forearm lift in which the barbell, held against the thighs, is raised to the chest and then lowered while keeping the legs, upper arms, and shoulders taut.b. a similar forearm lift using a dumbbell or dumbbells, usually from the side of the body to the shoulders.[1400-50; late ME, appar. back formation from curled, metathetic var. of ME crulled (ptp.) crul (adj.); cf. MD crullen to curl, CRULLER]
* * *
In mathematics, a differential operator that can be applied to a vector-valued function (or vector field) in order to measure its tendency to spin.It consists of a combination of the function's first partial derivatives. One of the more common forms for expressing it is: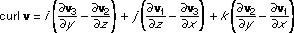 in which v is the vector field (v1, v2, v3), and v1, v2, v3 are functions of the variables x, y, and z, and i, j, and k are unit vectors in the positive x, y, and z directions, respectively. In fluid mechanics, the curl of the fluid velocity of the vector field (i.e., of the fluid itself) is called the vorticity or the rotation because it measures the field's tendency to rotate around a given point.
in which v is the vector field (v1, v2, v3), and v1, v2, v3 are functions of the variables x, y, and z, and i, j, and k are unit vectors in the positive x, y, and z directions, respectively. In fluid mechanics, the curl of the fluid velocity of the vector field (i.e., of the fluid itself) is called the vorticity or the rotation because it measures the field's tendency to rotate around a given point.* * *
Universalium. 2010.
