Fundamental laws of arithmetic
- Fundamental laws of arithmetic
-
Commutative law of addition: a + b = b + a
Associative law of addition: a + ( b + c ) = ( a + b ) + c
Commutative law of multiplication: a b = b a
Associative law of multiplication: a ( b c ) = ( a b ) c
Distributive law: a ( b + c ) = a b + a c
See as table: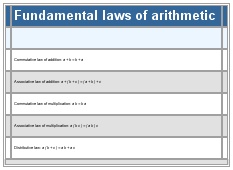
See as table: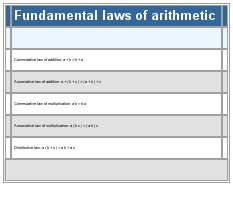
* * *
Universalium.
2010.
Look at other dictionaries:
arithmetic — arithmetically, adv. n. /euh rith meuh tik/; adj. /ar ith met ik/, n. 1. the method or process of computation with figures: the most elementary branch of mathematics. 2. Also called higher arithmetic, theoretical arithmetic. the theory of… … Universalium
Arithmetic — tables for children, Lausanne, 1835 Arithmetic or arithmetics (from the Greek word ἀριθμός, arithmos “number”) is the oldest and most elementary branch of mathematics, used b … Wikipedia
Laws of Form — (hereinafter LoF ) is a book by G. Spencer Brown, published in 1969, that straddles the boundary between mathematics and of philosophy. LoF describes three distinct logical systems: * The primary arithmetic (described in Chapter 4), whose models… … Wikipedia
Greek arithmetic, geometry and harmonics: Thales to Plato — Ian Mueller INTRODUCTION: PROCLUS’ HISTORY OF GEOMETRY In a famous passage in Book VII of the Republic starting at Socrates proposes to inquire about the studies (mathēmata) needed to train the young people who will become leaders of the ideal… … History of philosophy
History of algebra — Elementary algebra is the branch of mathematics that deals with solving for the operands of arithmetic equations. Modern or abstract algebra has its origins as an abstraction of elementary algebra. Historians know that the earliest mathematical… … Wikipedia
Musean hypernumber — Musean hypernumbers are an algebraic concept envisioned by Charles A. Musès (1919–2000) to form a complete, integrated, connected, and natural number system.[1][2][3][4][5] Musès sketched certain fundamental types of hypernumbers and a … Wikipedia
mathematics — /math euh mat iks/, n. 1. (used with a sing. v.) the systematic treatment of magnitude, relationships between figures and forms, and relations between quantities expressed symbolically. 2. (used with a sing. or pl. v.) mathematical procedures,… … Universalium
Mill, John Stuart: Logic and metaphysics — J.S.Mill Logic and metaphysics John Skorupski ENLIGHTENMENT AND ROMANTICISM IN MILL’S PHILOSOPHY Mill’s importance as one of the major figures of nineteenth century politics and culture, and the current interest in him as a moral and political… … History of philosophy
Emmy Noether — Amalie Emmy Noether Born 23 March 1882(1882 03 23) … Wikipedia
algebra — /al jeuh breuh/, n. 1. the branch of mathematics that deals with general statements of relations, utilizing letters and other symbols to represent specific sets of numbers, values, vectors, etc., in the description of such relations. 2. any of… … Universalium
 See as table:
See as table:
