- integration
-
/in'ti gray"sheuhn/, n.1. an act or instance of combining into an integral whole.2. an act or instance of integrating a racial, religious, or ethnic group.3. an act or instance of integrating an organization, place of business, school, etc.4. Math. the operation of finding the integral of a function or equation, esp. solving a differential equation.5. behavior, as of an individual, that is in harmony with the environment.6. Psychol. the organization of the constituent elements of the personality into a coordinated, harmonious whole.7. Genetics. coadaptation (def. 2).[1610-20; INTEGRATE + -ION; cf. L integratio renewal]Syn. 1. combination, blending, fusing.
* * *
The term, sometimes used interchangeably with "antidifferentiation," is indicated symbolically with the integral sign ∫. (The differential dx usually follows to indicate x as the variable.) The basic rules of integration are: (1) ∫(f + g)dx = ∫fdx + ∫gdx (where f and g are functions of the variable x), (2) ∫kfdx = k∫fdx (k is a constant), and (3)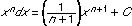 (C is a constant). Note that any constant value may be added onto an indefinite integral without changing its derivative. Thus, the indefinite integral of 2x is x2 + C, where C can be any real number. A definite integral is an indefinite integral evaluated over an interval. The result is not affected by the choice for the value of C. See also differentiation.
(C is a constant). Note that any constant value may be added onto an indefinite integral without changing its derivative. Thus, the indefinite integral of 2x is x2 + C, where C can be any real number. A definite integral is an indefinite integral evaluated over an interval. The result is not affected by the choice for the value of C. See also differentiation.* * *
in mathematics, technique of finding a function g(x) the derivative of which, Dg(x), is equal to a given function f(x). This is indicated by the integral sign “∫,” as in ∫f(x), usually called the indefinite integral of the function. (The symbol dx is usually added, which merely identifies x as the variable.) The definite integral, writtenwith a and b called the limits of integration, is equal to g(b) − g(a), where Dg(x) = f(x).Some antiderivatives can be calculated by merely recalling which function has a given derivative, but the techniques of integration mostly involve classifying the functions according to which types of manipulations will change the function into a form the antiderivative of which can be more easily recognized. For example, if one is familiar with derivatives, the function 1/(x + 1) can be easily recognized as the derivative of loge(x + 1). The antiderivative of (x2 + x + 1)/(x + 1) cannot be so easily recognized, but if written as x(x + 1)/(x + 1) + 1/(x + 1) = x + 1/(x + 1), it then can be recognized as the derivative of x2/2 + loge(x + 1). One useful aid for integration is the theorem known as integration by parts. In symbols, the rule is ∫fDg = fg − ∫gDf. That is, if a function is the product of two other functions, f and one that can be recognized as the derivative of some function g, then the original problem can be solved if one can integrate the product gDf. For example, if f = x, and Dg = cos x, then ∫x·cos x = x·sin x − ∫sin x = x·sin x − cos x + C. Integrals are used to evaluate such quantities as area, volume, work, and, in general, any quantity that can be interpreted as the area under a curve.* * *
Universalium. 2010.
